
Shutterstock.com
Statistics provide methods and tools for making decisions in uncertain or variable conditions, such as those produced from data collected during research. As study designs increase in complexity, interpreting the results using statistics becomes more difficult.
The purpose of this article is to provide pharmacists and healthcare professionals involved in research and report writing with an overview of basic statistical methods that can be applied to study data and used in reporting research results. One problem with statistics is that many terms have multiple names. This article will use the most commonly used statistical terms and in parentheses note common synonyms.
Planning research involves selecting an appropriate and important research question with measurable outcomes. Next, a single hypothesis or multiple hypotheses should be developed. These hypotheses will be critical to interpreting the results of the research. Thirdly, the researcher needs to identify the types of variables being studied, because these will determine the most appropriate statistical test, method of reporting the data or both. These three steps should be accomplished before commencing the study.
The data must be collected using a good sampling plan; recorded accurately; entered correctly into a computer program (chosen based on the type of variables studied); and analysed by appropriate software. However, the most important step is then making a decision based on the computer output. Here, the hypotheses will assist in interpreting the result for the study.
Box 1: Case study
A large hospital has three HMG-CoA reductase inhibitors (statins) on their hospital formulary. A study is designed where 120 patients newly diagnosed with hyperlipidaemia are randomly divided into three groups and each group of patients is administered one of the statins (statin A, statin B and statin C). After six months of therapy the change from baseline for each patient’s low-density lipoprotein (LDL) cholesterol is evaluated. In this case, the research question is: are there differences in responses based on the statin received?
Types of variables
One of the most important considerations is to identify the types of variables (factors) that will be seen in the research data. Variables can be divided into three classes: categorical, continuous and ordinal.
Categorical data (nominal classes) represents discrete groups with names; such as red or blue; experimental or control; or statin A, B or C, as in the case study (see ‘Box 1: Case study’). Continuous data involve information that is quantifiable, such as: weight, height, percent, blood pressure, blood urea nitrogen or change in low-density lipoprotein (LDL) cholesterol, as in the case study (Box 1).
Ordinal data have both categorical and continuous characteristics. Data are defined by categories — there is an order to these categories but the magnitude of difference between adjacent categories may not be equal or definable. For example, side effects can be classified as none, mild, moderate, severe or life threatening. The severity increases with increasing categories but it is difficult to show that the magnitude of difference is equal as levels change.
It is critical that the researcher identifies the class of variables because this will determine the most appropriate statistical method for evaluating the data. It is equally important that the researcher identifies those variables that are controllable.
Independent variables (predictor variables) are those factors controlled by the researcher. For example, volunteers for the cholesterol study (see box 1) will be assigned to one of three different statins. The independent variable in this case would be the statin to which the volunteer is assigned.
After six months of therapy, the change in LDL cholesterol observed in the volunteers is beyond the control of the researcher. The results seen for this “dependent” variable (outcome or response variable) is dependent on which of the three groups the volunteer has been assigned. So, in the case study in Box 1, there is a categorical independent variable with three levels (statin A, B or C) and a continuous dependent variable (change in LDL cholesterol); armed with these facts the researcher can determine the most appropriate statistical test to use.
Types of statistics
There are two basic types of statistics: descriptive and inferential. Descriptive statistics are the simplest type and involves taking the findings collected for sample data and organising, summarising and reporting these results. In many cases this will be all the information required for a research report.
With categorical or ordinal data, results can be reported as a frequency (count) or as a percentage (proportion) of each level of the variable. For example, in the case study there were 17 males (42.5%) that received statin A, 22 males (55.0%) received statin B and 19 males (47.5%) received statin C.
For continuous data, more information is available and reportable. Because it is a quantity that is being measured, there is information available not only about the average or middle of the continuous data — mode, median or mean — but how observations vary around that centre — range, variance or standard deviation, see Box 2 for definitions of measures of centre and dispersion.
Box 2: Measures of centre and dispersion
Centre:
- Mode – the observation with the greatest frequency or count;
- Median – that point at which half the observations fall below (50th percentile);
- Mean – the weighted centre, commonly referred to as the average.
NOTE– in a symmetrical bell shaped curve the mode = median = mean.
Dispersion:
- Range – the distance between the smallest and largest observation;
- Variance – the average of the squares of the deviation between each point and the mean;
- Standard deviation – the square root of the variance.
NOTE– because differences are squared and then taken as the square root, the values for the mean and the standard deviation are expressed in the same units of measure.
Sample reporting usually involves the mean and standard deviation. For instance, after six months of therapy the change in LDL cholesterol for statin A was -19.5 ± 16.3 mg/dl (mean ± standard deviation); whereas statins B and C showed smaller changes of -5.3 ± 12.8 and -4.6 ± 11.3 mg/dl, respectively. Assuming the researcher is careful and accurate in handling the data, these results can be assumed to be correct for that specific sample of volunteers.
Inferential statistics uses sample data (descriptive results) to make a prediction or inference about a larger population. In the example, it is possible to determine how the sample volunteers responded to either statin A, B and C with regard to their LDL cholesterol levels — can the same response be expected in a population of all patients receiving these drugs? Even with accurate sample results, the researcher cannot be completely confident in projecting the results to a population level.
However, using inferential statistics can control the risk of random error to a certain extent and the researcher can be 95% or 99% confident in the decision reached, allowing for only a 5% or 1% chance of being wrong with the final decision.
Testing hypotheses
At the outset of the study, two hypotheses are established. The first statement is the null hypothesis (hypothesis under test). In the case study the null hypothesis is that there is no difference in the average change in LDL cholesterol based on the statin received H0:
mA =
mB
=
mC. Here m represents population means (averages), which are being estimated based on sample means. The alternative hypothesis (research hypothesis) would be H1:H0 is false. Note these two hypotheses are always mutually exclusive and exhaustive; the outcome can only be one or the other and there are no other possible outcomes. The possible results of an inferential test are represented in Figure 1.
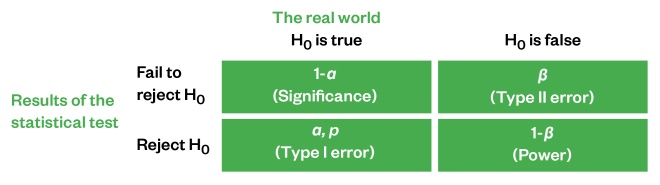
Figure 1: Possible results of inferential tests
Ideally, inferential statistical results will result in rejecting the hypothesis if it is actually false (1-β) or failing to reject the null hypothesis if it is actually true (1-α). Unfortunately, there is the possibility that errors can occur: accepting a false null hypothesis (β, Type II error) or rejecting a true null hypothesis (α, Type I error).
Ideally, inferential statistical results will result in rejecting the hypothesis if it is actually false (1-β) or failing to reject the null hypothesis if it is actually true (1-α). Unfortunately, there is the possibility that errors can occur: accepting a false null hypothesis (β, Type II error) or rejecting a true null hypothesis (α, Type I error).
For the case study example, this means that accepting that the type of statin given had no effect on LDL cholesterol levels when, in fact, it does would be a Type II error. Believing that one statin had a greater effect on LDL cholesterol levels than the other two statins when, in fact, there is no difference between the statins would be a Type I error.
Type I error is the easiest to control because the researcher can set a limit of acceptable error (e.g., a = 0.05 or 0.01) by selecting a value from a statistical table. This a is determined a priori (before the study) as a level of confidence. If a computer is used for the inferential test, the output will give a p -value — this is the exact probability of a Type I error the researcher must accept in rejecting the null hypothesis.
In the case study with the three statins the result of the test would be p <0.001. In other words, if the researcher rejects the null hypothesis (H0) that all the statins are equal, the chance of being wrong is less than 0.1%. If the researcher was interested in gender as a variable of interest, then the results for all volunteers based on gender would be p =0.321. In this case, to say there is a difference based on gender the error rate would be an unacceptable 32% so the researcher would have to report a failure to find a significant difference (and therefore fail to reject the null hypothesis).
It is important to note that one can never prove the null hypothesis but simply fail to reject it. It is a subtle difference but failing to reject the null hypothesis does not prove that the three statins are equally effective.
Sample size is based on the power (1-β) desired for a study. The power is the probability of rejecting the null hypothesis when it is actually false for the population. Sample size is based on a variety of equations each involving: acceptable Type II error (usually 0.20), a priori Type I error (often 0.05), a defined difference that the researcher considers significant (e.g., clinically significant) and the amount of variability in the data (this is extremely difficult to estimate if it is the first time a study of a particular nature is attempted). The best advice is to seek assistance from a professional statistician to determine an appropriate sample size. Alternatively, guess the sample size, run the test and determine the power after the fact based on the variability of the sample data (for example, the study was powered to 0.83; the probability that the researcher is correct in rejecting the null hypothesis).
Selecting the most appropriate clinical test
As noted earlier, the types of variables will help determine the best statistical test to use for the research report. If the report involves only descriptive statistics for the sample data, frequencies and percentages would be used for categorical data and measures of average and dispersion for continuous data.
For inferential statistics, a guide is presented in ‘Table 1: Basic inferential statistical tests and associated variables’. Inferential tests used to identify differences include the t-tests or the analysis of variance (ANOVA) whereas correlation, regression or chi-square tests can be used to identify relationships. There are hundreds of other inferential tests, but most are modifications or extensions of the basic tests in Table 1. Ordinal data are handled using the same tests as categorical data or by non=parametric procedures, which are beyond the scope of this article.
| Table 1: Basic inferential statistical tests and associated variables | ||
|---|---|---|
| Independent variable | Dependent variable | Statistical tests |
| Categorical | Continuous | Confidence intervals t-tests (paired and unpaired), analysis of variance (ANOVA) |
| Categorical | Categorical | Chi-Square test of independence, z-test of proportions, odds ratios, relative risk ratio |
| Continuous | Continuous | Correlation, regression |
Useful Resources:
De Muth JE. Clinical research: preparing for the first meeting with a statistician. Am J Health Syst Pharm 2008;65(24):2358–2366.
De Muth JE. Clinical research: an overview of biostatistics. Am J Health Syst Pharm 2009;66(1):70–81.
Conflicts of interest disclosure:
James E De Muth is the author of a reference book on on pharmaceutical statistics titled Basic Statistics and Pharmaceutical Statistical Applications, Third Edition.
Reading this article counts towards your CPD
You can use the following forms to record your learning and action points from this article from Pharmaceutical Journal Publications.
Your CPD module results are stored against your account here at The Pharmaceutical Journal. You must be registered and logged into the site to do this. To review your module results, go to the ‘My Account’ tab and then ‘My CPD’.
Any training, learning or development activities that you undertake for CPD can also be recorded as evidence as part of your RPS Faculty practice-based portfolio when preparing for Faculty membership. To start your RPS Faculty journey today, access the portfolio and tools at www.rpharms.com/Faculty
If your learning was planned in advance, please click:
If your learning was spontaneous, please click:



