A guide to rounding for pharmacy students and trainees

Rounding is an area that many pharmacy students and trainee pharmacists struggle with. In the General Pharmaceutical Council (GPhC) registration assessment, if there are no rounding instructions at the end of a question, it is because the worked answer is already a whole number (so no rounding is needed). If there are no rounding instructions at the end of a question and a worked answer is not a whole number, then the answer is wrong and the question must be attempted again.

Some questions, while requiring a whole-number answer, may still require rounding in the middle of a question. Please also refer back to the official GPhC example questions. Mock papers are not official and may give inaccurate rounding advice. The rule when rounding is that a number that is 5 or above should be rounded up, and anything below 5 is rounded down. This rounding rhyme might help candidates to remember: 5 or more? Let it soar. 4 or less? Let it rest.

Below are some example questions which can be used to prepare for the registration assessment.

Rounding exercises

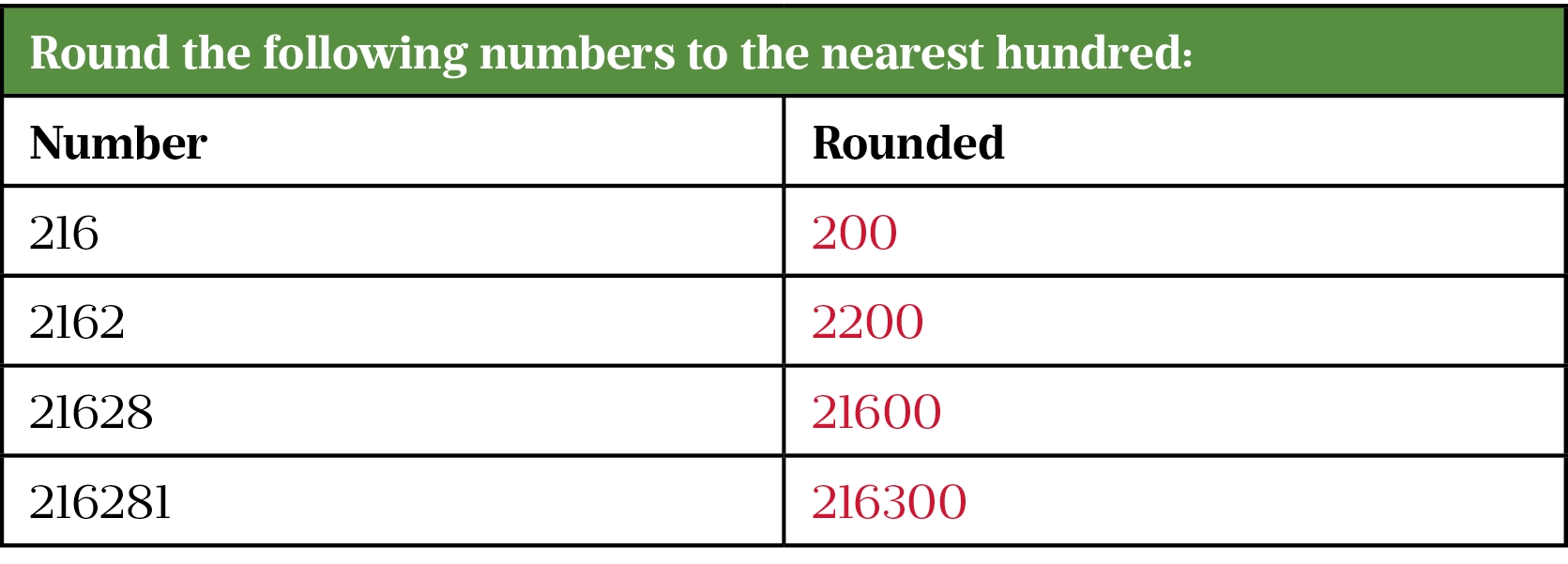
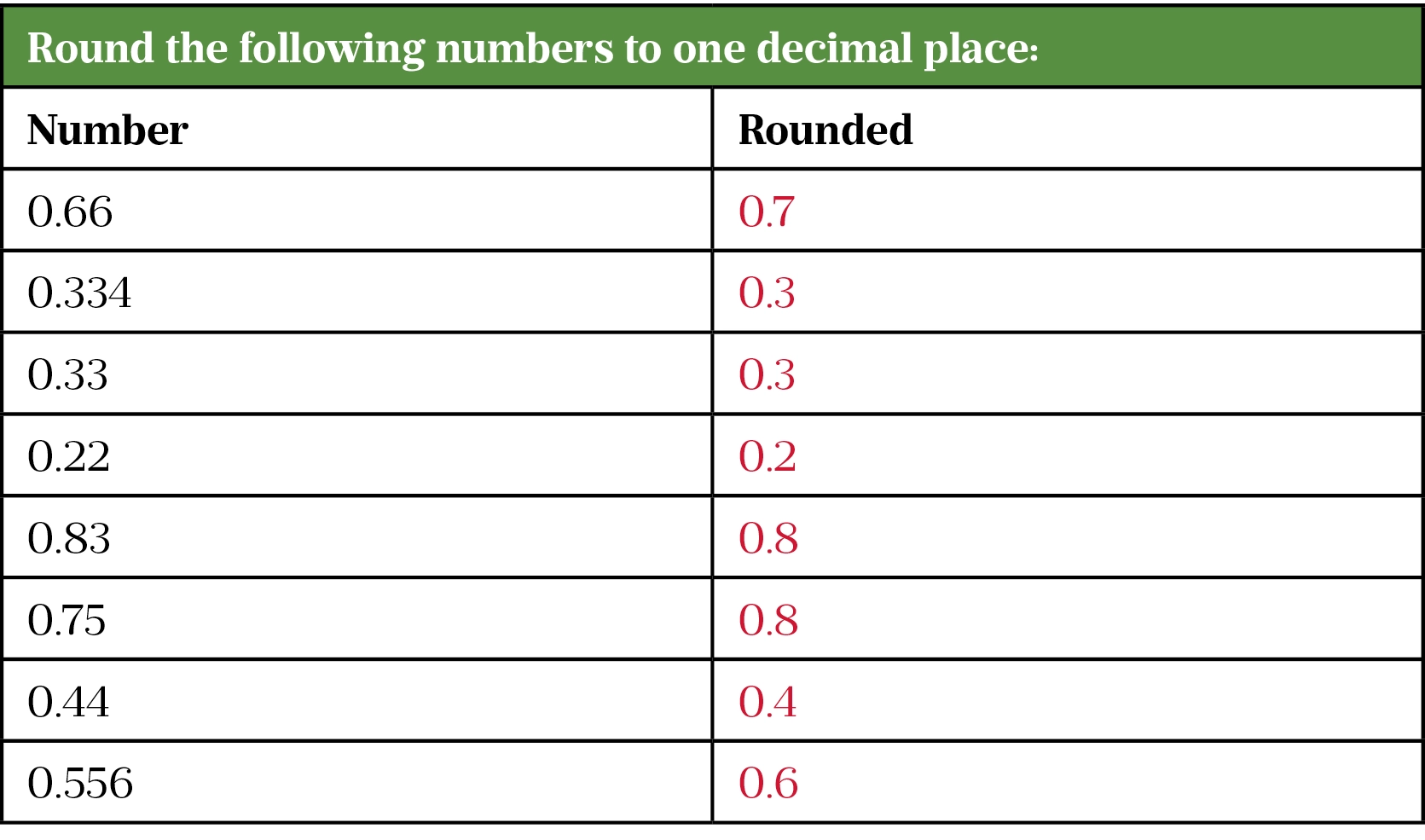
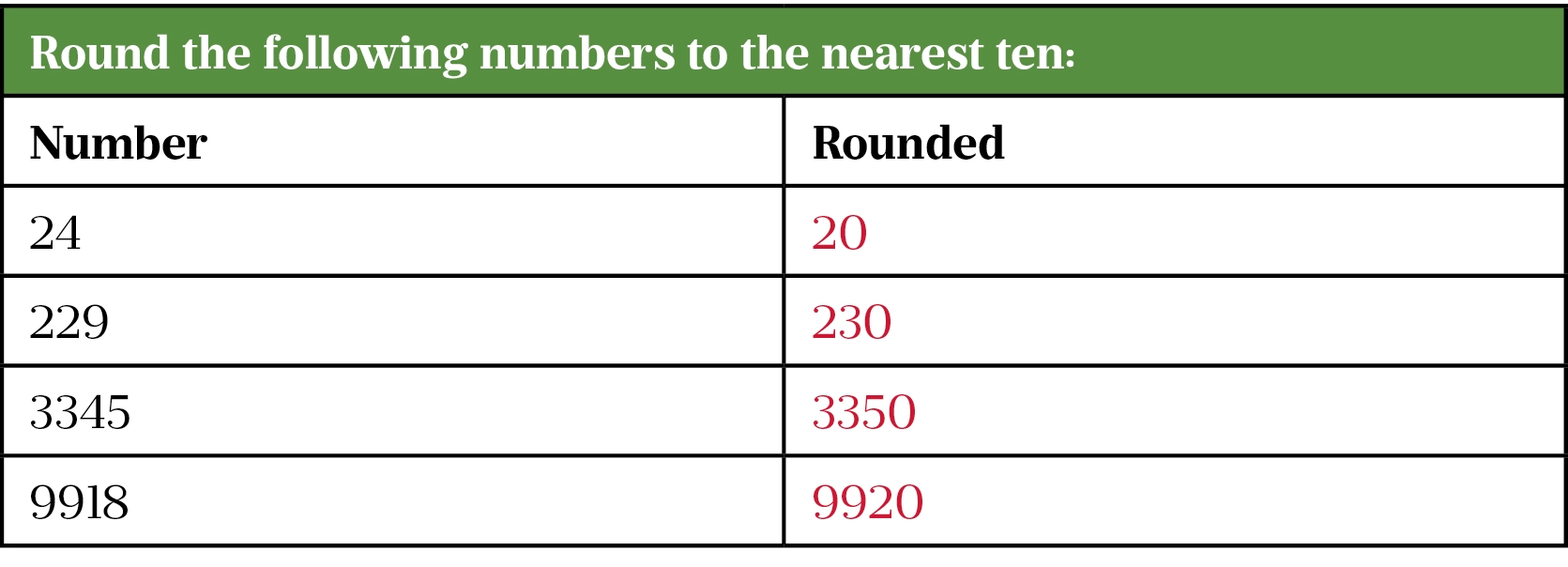
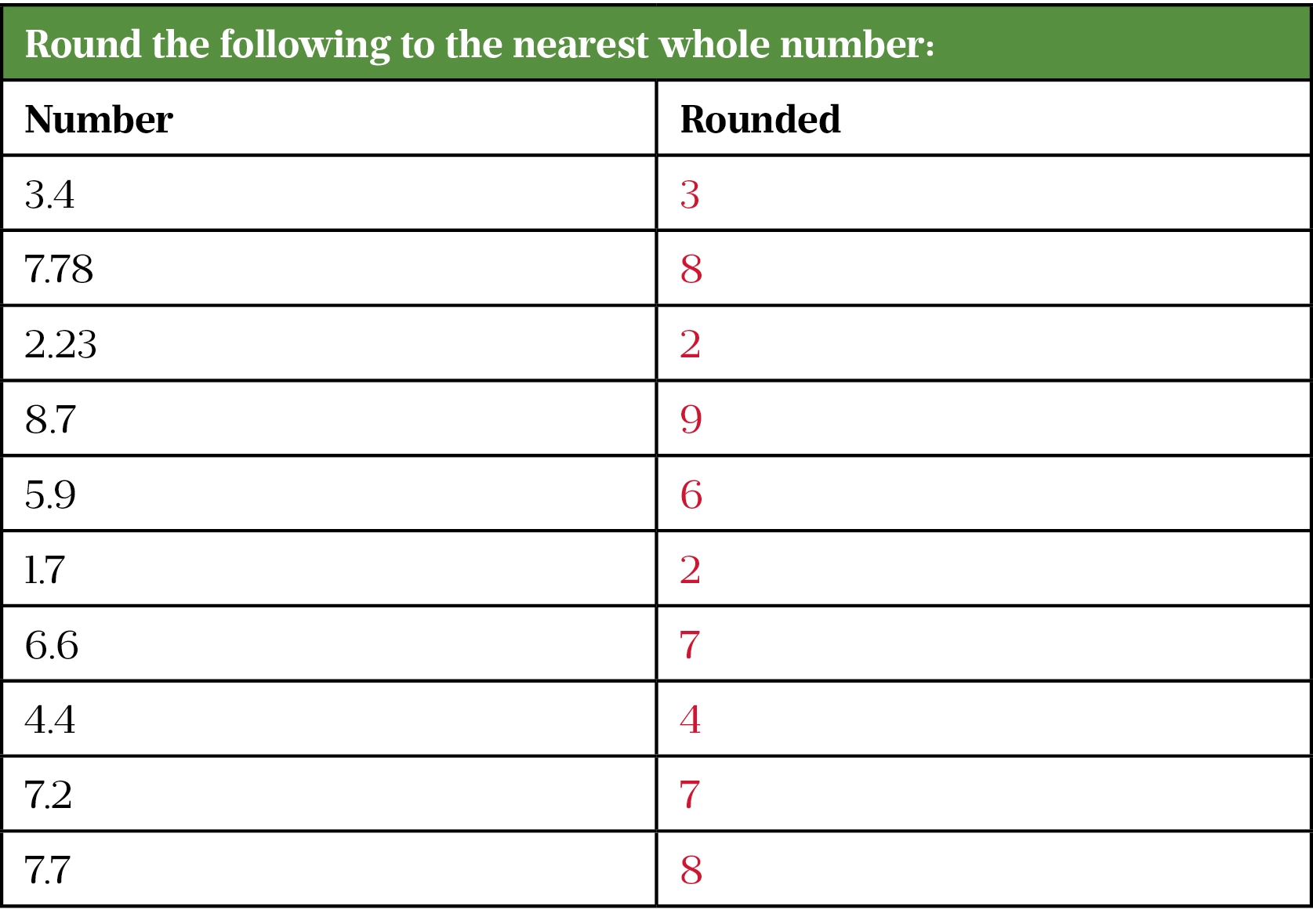
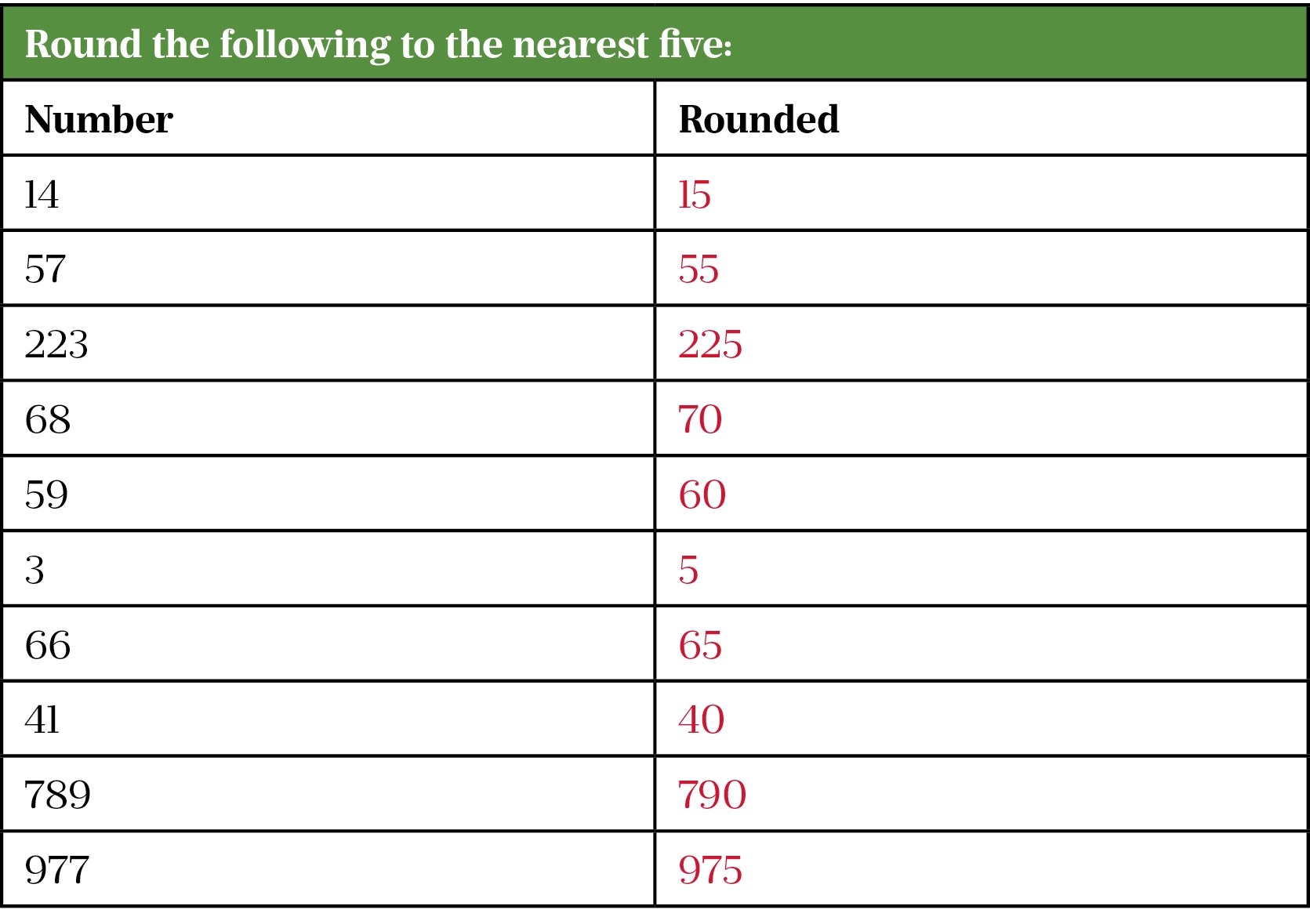
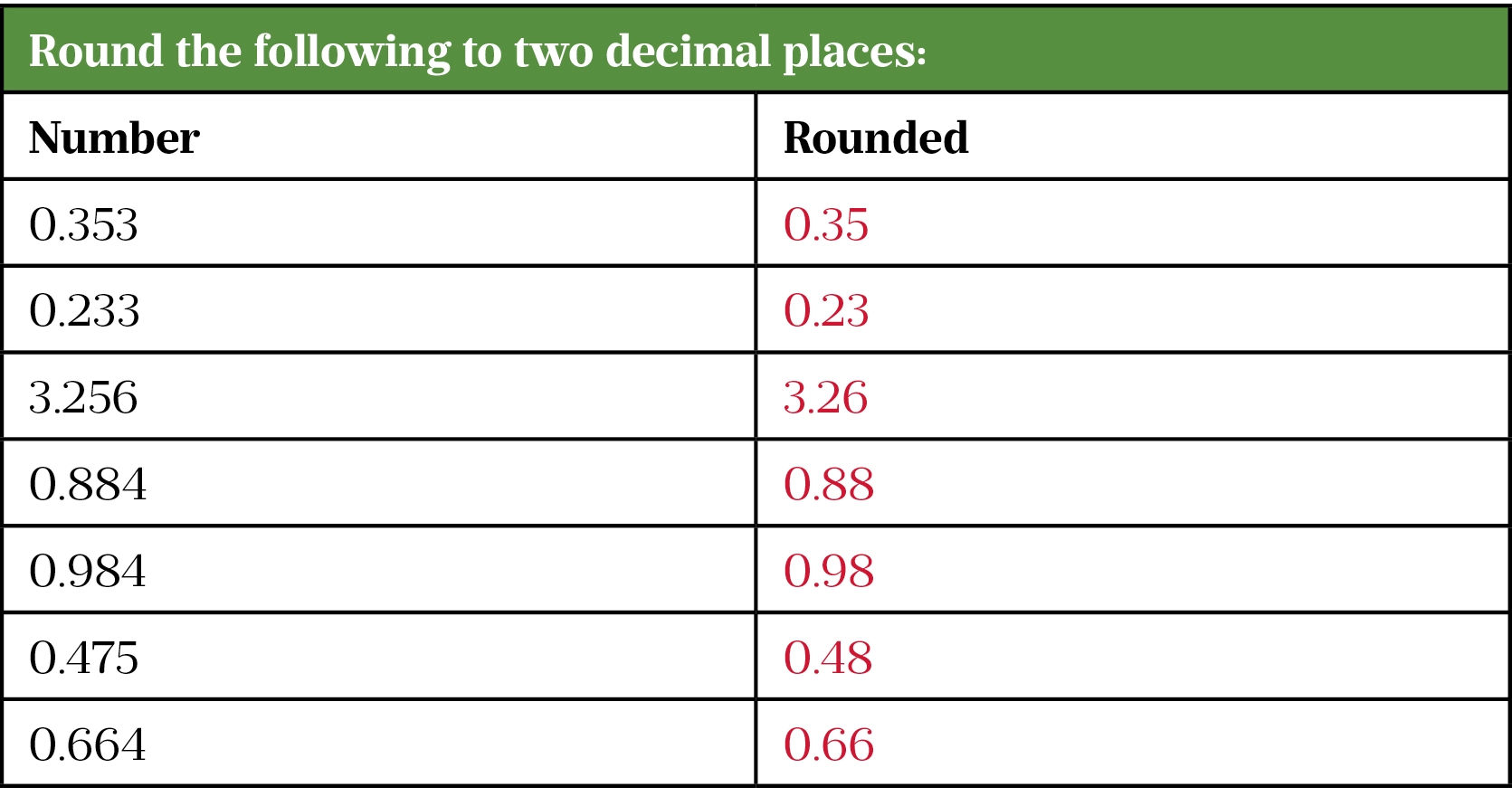
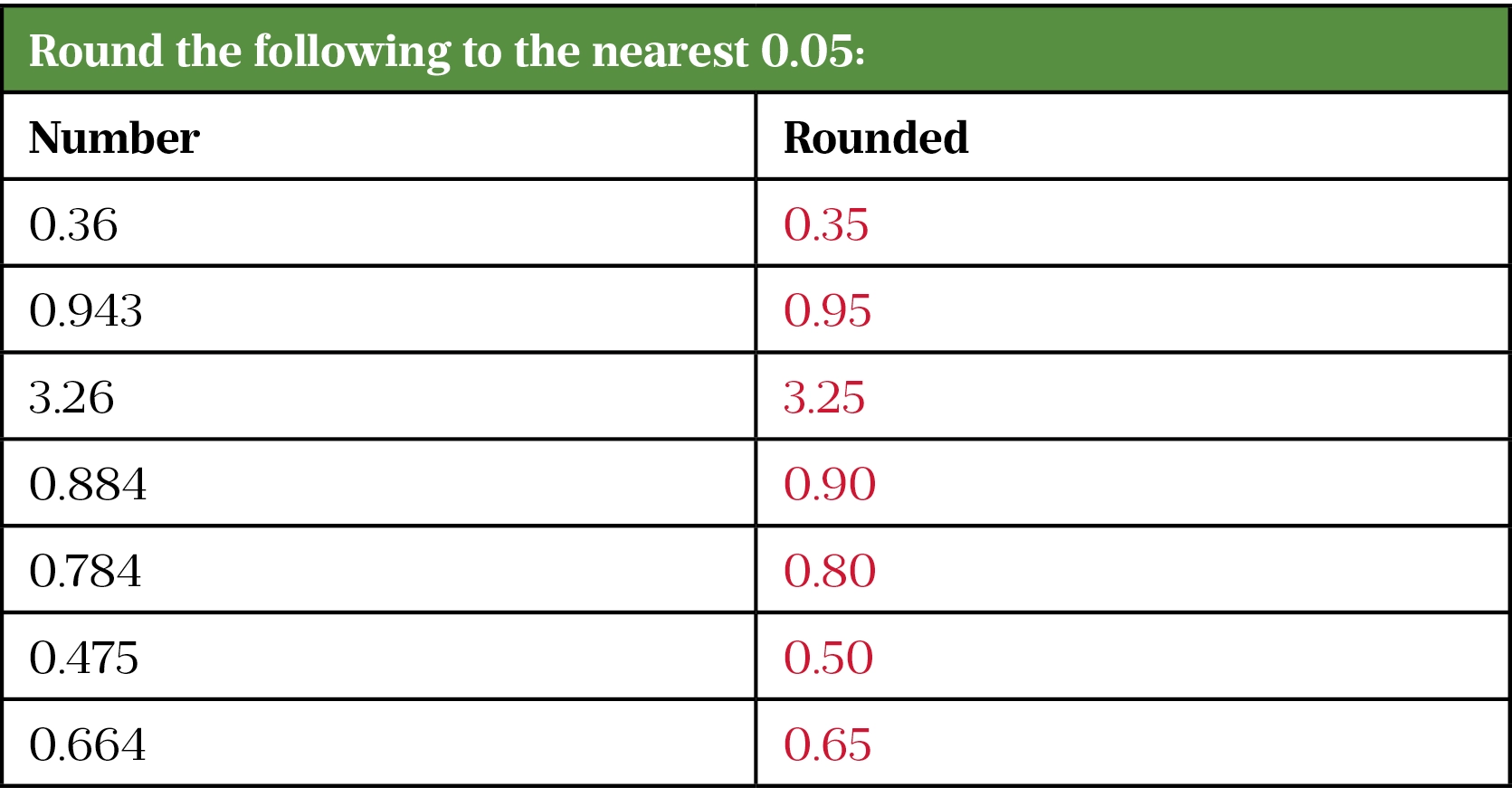
Rounding example questions

Here are five questions that illustrate when to round in different situations and when rounding is not needed.

Question 1

A woman aged 45 years has a percutaneous endoscopic gastrostomy tube in situ. She requires 1600kcal per 24 hours from her enteral feed and has been instructed to use Nutrison Energy, which contains 150kcal per 100mL. She would like to feed for 14 hours overnight.

At what rate in mL/hour should this feed be delivered? Give your answer to the nearest whole number.

Step 1: Understand that we have to round our worked answer to the nearest whole number. Highlight the rounding information in the assessment.

Step 2: Work out how many kcal/mL there is in Nutrison Energy

100mL ÷ 150kcal = 1.5kcal/mL

Step 3: Work out the quantity of Nutrison Energy that will deliver 1600kcal

1600kcal ÷ 1.5kcal/mL = 1066.66666mL

Step 4: Work out the rate in mL/hr

Our patient is receiving 1600 kcal per 24 hours but this is being delivered in only 14 hours

1066.66666mL ÷ 14 hours = 76.19mL/hr

Step 5: Round to the nearest whole number

We have been instructed to round to the nearest whole number.

Note: Do not add units in the answer box.

Answer: 76

Question 2

A man aged 52 years, who weighs 63kg, attends a pre-admission clinic at hospital two weeks prior to having orthopaedic surgery. He has moderate anaemia and his doctor prescribes a course of subcutaneous Eprex (epoetin alfa). The Eprex is given at a dose of 300 units/kg daily for 15 days.

How many units of Eprex will he be given, in total, during the 15-day course?

Step 1: Understand that because there are no rounding instructions, the correct answer will be a whole number. No rounding is needed at the end.

Step 2: Work out his daily dose

300 units x 63kg = 18900 units/day

Step 3: Work out the number of units for 15 days

18900 units x 15 days = 283500 units

Note: Do not add commas when inputting your answer in the answer box.

Answer = 283500

Question 3

A girl aged 7 years, who weighs 19kg, is prescribed clobazam 250µg/kg twice daily as adjunctive maintenance therapy for epilepsy. To aid administration of this medicine, her parents have been advised that each dose should be rounded to the nearest whole mL.

How many mL of clobazam 10mg/5mL oral suspension are needed for two weeks’ treatment?

Step 1: Understand that because there are no rounding instructions that the correct answer will be a whole number. No rounding is needed at the end.

Step 2: Work out single dose

19kg x 250µg = 4750µg

Step 3: Convert to mg as our suspension is in mg/mL

4750µg ÷ 1000 = 4.75mg

Step 4: Work how much clobazam 10mg/5mL oral suspension is needed per dose

5mL ÷ 10mg x 4.75mg = 2.375mL

Step 5: Round to the nearest whole mL as stated in the scenario.

2.375mL = 2mL

Rounding instructions may be included in the scenario and not at the end.

Step 6: Work out quantity needed per day in mL

2mL x two doses per day = 4mL per day

Step 7: Work out quantity needed for two weeks

4mL x 14 days = 56mL

Answer = 56

Question 4

A patient requires treatment with a cytotoxic medicine at a dose of 22mg/m² daily for three days. The patient weighs 76kg and is 1.74m tall.

How many 20mg capsules of this cytotoxic medicine are needed for the five-day course of treatment?

Step 1: Understand that because there are no rounding instructions that the correct answer will be a whole number. No rounding is needed at the end.

Step 2: Convert height into cm

1.74m = 174cm

Step 3: Work out body surface area

76kg x 174cm÷ 3600 = 3.6733333

Square rooted = 1.9165941

Step 4: Work out dose

1.9165941 x 22mg = 42.165068mg daily

Step 5: Round to the nearest capsule

We round to 40mg because the capsules are available as 20mg

Step 5: Work out number of capsules for five days

2 capsules per day x 5 days = 10

Answer = 10

Question 5

You are working as a practice pharmacist and have been asked to help reduce expenditure on medicines. You are reviewing the use of Combodart (tamsulosin hydrochloride 400µg and dutasteride 500µg) capsules as it is more cost effective to prescribe the individual generic components, as capsules, separately. Combodart should be reserved for patients with compliance problems for whom reducing the overall tablet burden would improve patient safety.

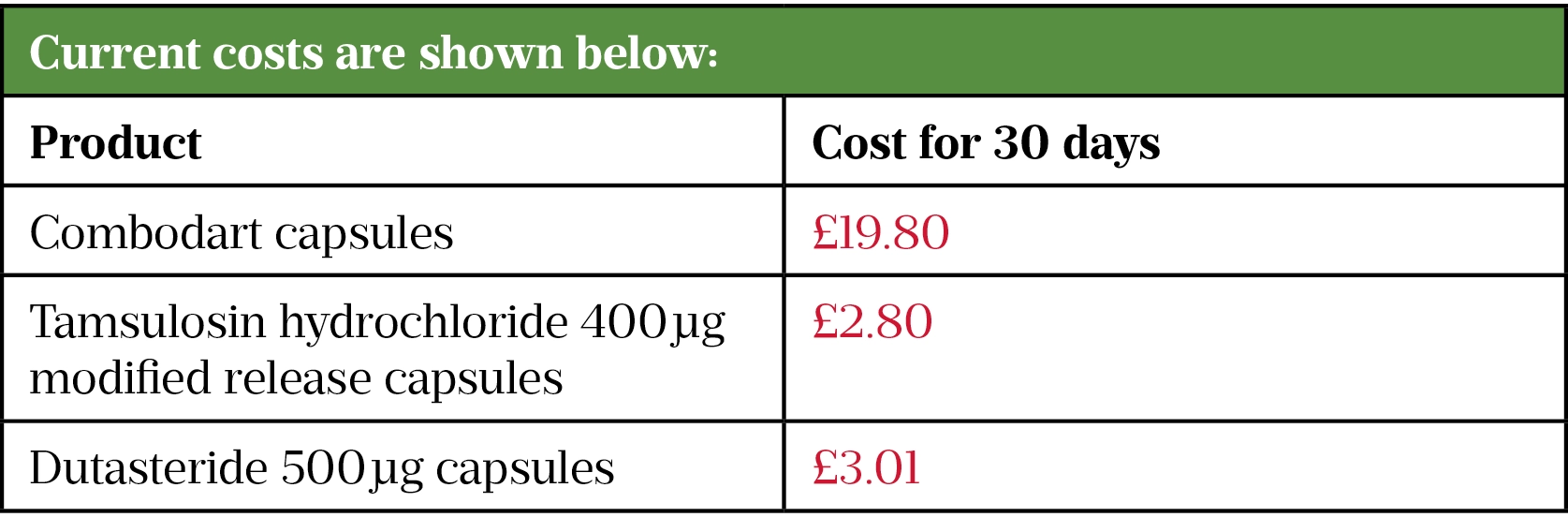
After reviewing 120 patients on repeat prescriptions for Combodart, you have identified that 75% of them could potentially switch to using the individual generic components without impacting patient safety. The practice has a repeat prescribing policy of 30 days treatment on a prescription for this product.

What is the total saving for the practice per month, assuming all of the suitable patients switch to using the separate generic products? Give your answer to the nearest £5.

Step 1: Understand that we will have to round our worked answer to the nearest £5.

Step 2: Work out the number of suitable patients

75% of 120 = 90

Step 3: Cost saving for one patient per month

£19.80 – £2.80 – £3.01 = £13.99

Step 4: Cost saving for 90 patients per month

£13.99 x 90 = £1259.1

Step 5: Round to the nearest £5

£1260

Answer = 1260